UNIDAD 1
LÓGICA
La lógica es la disciplina que trata de los métodos, modos y formas de razonamiento humano.Ofrece reglas y técnicas para determinar si el argumento es válido o no.Una de las metas fundamentales de la lógica es eliminar la amigue dad de un lenguaje ordinario, introduciendo símbolos y conectivos lógicos en la construcción de proposiciones. Tanto que las proposiciones son la base del razonamiento lógico que consiste en decidir la valides de una idea en base a un enunciado que previamente fueron aceptados.
PROPOSICIONES.- Una proposición en toda oración o enunciado respecto del cuál se puede definir si es verdadero o falso pero no ambos a la vez. Es decir todo proposición esta asociada a un valor de verdad la cual puede ser Verdadero o Falso así unas proposiciones Verdaderas, es falso si su valor de verdad es Falso.
NOTA.- Una proposición es una oración al que tiene un solo valor de verdad en el transcurso del tiempo o cualquiera se el lugar, donde este utilizando dicha proposición.
Ejemplo:
Determinar cual de las siguientes oraciones son proposiciones.
⧪Cuál es tu nombre No
⧪5 + 4 = 8 Si
⧪El ser humano es el arquitecto de su propio destino Si
⧪El símbolo H2O es del Agua Si
NOTACIONES Y CONECTIVOS LÓGICOS.- A las proposiciones simples o genéricas (atómica) se acostumbran de notas por las letras minúsculas p,q,r...por parte así por ejemplo:
PROPOSICIONES.- Una proposición en toda oración o enunciado respecto del cuál se puede definir si es verdadero o falso pero no ambos a la vez. Es decir todo proposición esta asociada a un valor de verdad la cual puede ser Verdadero o Falso así unas proposiciones Verdaderas, es falso si su valor de verdad es Falso.
NOTA.- Una proposición es una oración al que tiene un solo valor de verdad en el transcurso del tiempo o cualquiera se el lugar, donde este utilizando dicha proposición.
Ejemplo:
Determinar cual de las siguientes oraciones son proposiciones.
⧪ Los gatos hablan Si
⧪Mañana sale el sol No⧪Cuál es tu nombre No
⧪5 + 4 = 8 Si
⧪El ser humano es el arquitecto de su propio destino Si
⧪El símbolo H2O es del Agua Si
NOTACIONES Y CONECTIVOS LÓGICOS.- A las proposiciones simples o genéricas (atómica) se acostumbran de notas por las letras minúsculas p,q,r...por parte así por ejemplo:
p: "Los gatos hablan" F
q: "La tierra es esférica" V
↝p: V
↝q: F
A partir de proposiciones simples se pueden generar otras proposiciones simples se pueden generar otras proposiciones simples o compuestas utilizando cierta constantes proposicionales llamados conectivos lógicos tales como:


ÁLGEBRA DE PROPOSICIONES.- Son operaciones lógicas que se realizan en una fórmula proposicional aplicando adecuadamente ciertas reglas básicas llamadas leyes lógicas. Es decir como el algebra básica donde la simplificación de expresiones algebraicas es muy importante en lógica también existe la necesidad de simplificar fórmulas proposicionales completas a través de ciertas equivalencias llamadas leyes lógicas.
LEYES LÓGICAS
CIRCUITOS LÓGICOS.- Circuito con un interruptor puede estar abierto o cerrado cuando el interruptor esta abierto no permite paso de corriente mientras cuando está cerrado sí lo permite y asociamos proposición a cada interruptor, intuitivamente, vemos que en el algebra de circuitos la V de tal proposición indica el interruptor cerrado y F el interruptor abierto.
el conectivo No en símbolo "↝"
el conectivo Y se denota "⋀"
el conectivo O se denota "⋁"
el conectivo Sí...entonces, se denota "⟶"
el conectivo Sí y solo sí, se denota "⟺"
el conectivo O excluyente, se de nota "⊻"
OPERACIONES PROPOSICIONALES.- Cada una o dos proposiciones cuyo valor de verdad se conoce las operaciones entre proposiciones y caracterizar la proposición resultante a través de su valor de verdad.
Estas son las negaciones:
Negación "~"
Conjunción "⋀"
Disyunción "⋁"
Implicación "⟶"
Doble implicación "⟺"
Disyunción exclusiva "⊻"
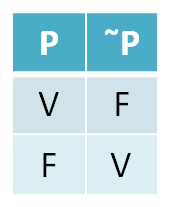
➤NEGACIÓN.- Si una proposición P se llama negación de V a la proposición que se obtiene uniendo el conectivo no. Se denota por "no P", en símbolo "~P".
Su tabla de valor de verdad.

P: "Los gatos hablan" F
~P: "Los gatos no hablan" V
~P: "Los gatos no hablan" V
➤CONJUNCIÓN.- Se llama conjunción de dos proposiciones p y q a la proposición que se obtiene uniendo por medio del conectivo Y, se escribe, "p ⋀ q", se lee "p y q".

NOTA.- El valor de verdad de la conjunción es verdadero si ambos valores de verdad son verdaderos caso contrario es falso.
➤DISYUNCIÓN.- La disyunción de dos proposiciones p y q se llama a la proposición que se obtiene uniendo por medio de conectivo O, se escribe "p y q" y se lee "p o q".

NOTA.- El valor de la disyunción p o q es falso si ambos valores de dichas proposiciones son falsos caso contrario es verdadero.
➤IMPLICACIÓN.- Se llama implicación de dos proposiciones p y q a la proposición que se obtiene uniéndolas por medio del conectivo "sí entonces", se escribe p ⟶ q y se lee "si p entonces q".Donde p es la proposición llamada antecedentes y q proposición consecuente. 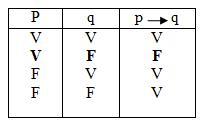

NOTA.-El valor de verdad de la implicación entre p y q es falso si el antecedente, es verdadero y el consecuente es falso caso contrario el valor de verdad de la implicación es verdadero.
Definición de implicación p ⟶ q = ~p ⋁ q.
➤DOBLE IMPLICACIÓN.- Se llama doble implicación de dos proposiciones p y q a la proposición que se obtiene uniéndola por medio de conectivo sí y solo sí "se escribe "p⟺q"se lee p si y solo si q"
NOTA.- El valor de verdad de la doble implicación entre p y q es verdadero si ambos tienen el mismo valor de verdad caso contrario es falso.
Definición p ⟺ q = (p ⟶ q) ⋀ (q ⟶ p)
➤DISYUNCIÓN EXCLUSIVA.- Se llama disyunción exclusiva de dos proposiciones p y q a la proposición que se obtiene uniéndolas por medio del conectivo o excluyente se escribe "p ⊻ q" se lee "p excluye a q".

NOTA.- El valor de verdad de la disyunción exclusiva entre p y q es verdadero si los valores de verdad son diferentes (opuestos), caso contrario es falso.
Definición p ⊻ q = ~(p ⟺ q)
FORMULAS PROPOSICIONALES.- Una formula proposicional es una combinación de proposiciones y conectivos lógicos que simboliza una proposición compuesta o molecular.
⧭[(p ⟶(q ⋁ r)] ⟺ [(p ⋁ q) ⋀ r]
⧭(p ⟶ q) ⟶ r
TABLA DE VALORES DE VERDAD.- El valor de verdad de una formula proposicional depende de los valores de verdad de las proposiciones simples que la componen. Es decir se debe analizar todas las posibles combinaciones de valores de verdad que las proposiciones que la componen las cuales se dan en las primeras columnas. Por tanto si en una formula proposicional intervienen "N" proposiciones el número de proposiciones para la tabla valor de verdad se calcula con 2 elevado a n.
[(p⋀r) ⟺ (~q⋁r)]=2³=8

CLASIFICACIÓN DE FORMULAS PROPOSICIONALES.- Las formulas proposicionales se clasifican según el valor de verdad de la columna resultante como: tautología,contradicción y contingencia.

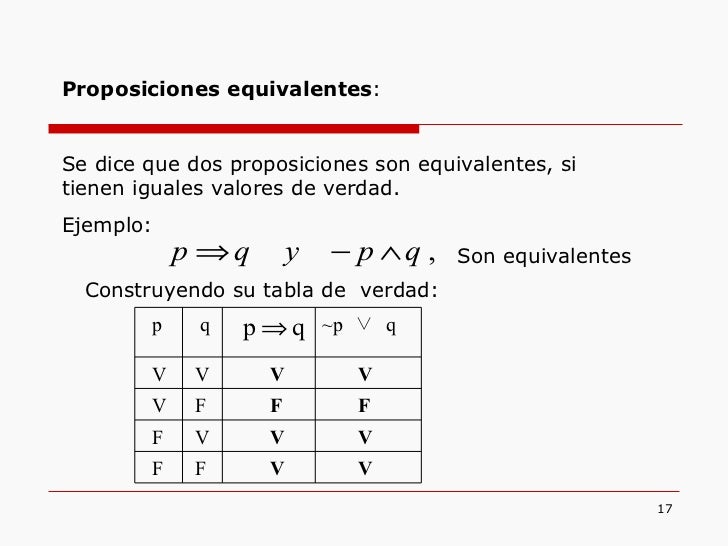
EQUIVALENCIA LÓGICA.- Dos fórmulas proposicionales son lógicamente equivalentes si su tabla de verdad se expresan de la misma forma. Ejemplo:
TABLA DE VALORES DE VERDAD.- El valor de verdad de una formula proposicional depende de los valores de verdad de las proposiciones simples que la componen. Es decir se debe analizar todas las posibles combinaciones de valores de verdad que las proposiciones que la componen las cuales se dan en las primeras columnas. Por tanto si en una formula proposicional intervienen "N" proposiciones el número de proposiciones para la tabla valor de verdad se calcula con 2 elevado a n.
[(p⋀r) ⟺ (~q⋁r)]=2³=8
CLASIFICACIÓN DE FORMULAS PROPOSICIONALES.- Las formulas proposicionales se clasifican según el valor de verdad de la columna resultante como: tautología,contradicción y contingencia.
- TAUTOLOGIA.- Es una formula proposicional que es verdadera para cualquier combinación de proposiciones de entrada de dicha fórmula proposicional.
- CONTRADICCIÓN.- Es una formula proposicional que es falso para cualquier combonación de entrada de dicha formula proposicional.
- CONTINGENCIA.- Es una fórmula proposicional que no es ni tautología ni contradicción.

EQUIVALENCIA LÓGICA.- Dos fórmulas proposicionales son lógicamente equivalentes si su tabla de verdad se expresan de la misma forma. Ejemplo:

ÁLGEBRA DE PROPOSICIONES.- Son operaciones lógicas que se realizan en una fórmula proposicional aplicando adecuadamente ciertas reglas básicas llamadas leyes lógicas. Es decir como el algebra básica donde la simplificación de expresiones algebraicas es muy importante en lógica también existe la necesidad de simplificar fórmulas proposicionales completas a través de ciertas equivalencias llamadas leyes lógicas.
LEYES LÓGICAS
- Ley Idempotencia = p ⋀ p = p , p ⋁ p = p
- Ley conmutativa = p⋀q=q ⋀ p . p ⋁ q=q⋁ p
- Ley asociativa = p ⋁ (q ⋁ r)=(p ⋁ q) ⋁ r , p ⋀ (q ⋀ r)=(p⋀ q) ⋀ r
- Ley de negación = ~ (~ p)=p, p⋀~ p=F, p ⋁~ p=V
- Ley de identidad = p ⋀ V=p, p ⋁ F= p
- Ley de morgan =~(p ⋁ q)= ~p ⋀ ~q, ~ (p⋀ q) =~ p ⋁ ~ q
- Definición implicación = p ⟶ q= ~ p ⋁ q
- Ley distributiva = p ⋁ (q ⋀ r)=(p⋁ q)⋀ ( p ⋁ r),p⋀ (q⋁ r) = ( p⋀ q) ⋁ (p ⋀ r)
- Ley de absorción = p⋁ (p⋀ q)=p, p ⋀ (p⋁ q)=p, p⋀ F=F. p ⋁ V=V
- Definición doble implicación = (p ⟺ q)= (p ⟶ q) ⋀ (q ⟶ p)
- Definición de disyunción exclusiva = (p ⊻ q)= ~ (p⟺ q)
CIRCUITOS LÓGICOS.- Circuito con un interruptor puede estar abierto o cerrado cuando el interruptor esta abierto no permite paso de corriente mientras cuando está cerrado sí lo permite y asociamos proposición a cada interruptor, intuitivamente, vemos que en el algebra de circuitos la V de tal proposición indica el interruptor cerrado y F el interruptor abierto.
- CIRCUITOS EN SERIE Y PARALELO.- Las operaciones proposicionales se pueden representar mediante circuitos lógicos con tantos interruptores como proposiciones que la componen combinados en serie o en paralelo según el conectivo lógico que une las proposiciones.
- CIRCUITOS EN SERIE.- La conjunción de dos proposiciones (p⋀q) está representada por el circuito lógico en series.
- CIRCUITO PARALELO.- La disyunción de dos proposiciones (p⋁q) está representada por un circuito lógico en paralelo.
INFERENCIA LÓGICA.- Se debe entender por inferencia lógica a un razonamiento válido en el que a partir de un conjunto de proposiciones llamadas premisas se obtienen un resultado llamado conjunción de las premisas implica la conjunción. Es decir si las premisas son todas verdaderas, entonces la conclusión que derivan de ella lógicamente serán verdadera, caso contrario si una o más premisa es falso la conclusión también sera falso.
REGLAS DE INFERENCIA.- Se llama regla de inferencia a todo argumento universalmente correcto que representa métodos generales de razonamiento válido.
FUNCIONES PROPOSICIONALES Y SUS CUANTIFICADORES
- FUNCIÓN PROPOSICIONAL.- Una función proposicional en una variable x es toda expresión en la que x representa al sujeto u objeto perteneciente a cierto conjunto. La cual se convierte en proposición para cada especificación de x. Es decir si P(x) es una expresión que se convierte en proposición al sustituir la variable x por un objeto matemático se dice que P es una función proposicional.Así mismo hay funciones proposicional con más de una variable.
- CUANTIFICADORES.- A partir de funciones proposicionales se puede obtener funciones generales proposiciones generales mediante un metodo o proceso llamado cuantificación. Para ello introducimos los siguientes símbolos ∀, Ǝ llamados cuantificadores universal y existencial respectivamente.
Ǝ : Existencial
∀x; "Para todo x "5" cualquiera que sea x"
Ǝx: "Existe algún x, talque "o" existe al menos un x, tal que "
Sea vocales = {a,e,i,o,u}
∀x: "x es vocal"
Ǝx: "x/x es vocal fuerte"
∀x: P(x) se lee "para todo x, se verifica P(x)"
Ǝx: P(x) se lee "existe algún x, tal que se verifica P(x)"
NEGACIÓN DE CUANTIFICADORES
~(∀x:P(x) = Ǝx/~P(x)
~(Ǝx/P(x) = ∀x:~P(x)
Ejemplo:
Expresar utilizando cuantificadores.
P(x): "Alumno que estudia una materia"
q(x): "Alumno aprueba la materia"
∀x: P(x) → q(x)
Negación
~(∀x: P(x) → q(x) = Ǝx/~(P(x) → q(x))
= Ǝx/~(~P(x) ⩗q(x))
= Ǝx/ P(x) ~q(x)
Existe alumno que estudia y no aprueba la materia.
No hay comentarios:
Publicar un comentario